| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 싱글톤패턴
- bean
- Spring
- Velog
- publicapi
- 인수테스트
- SOLID
- 클라이언트사이드렌더링
- DI
- 더티채킹
- 항해99 9기
- 항해99
- java
- 다형성
- 변경감지
- 지네릭스
- refreshtoken
- 일급컬렉션
- 9기
- 애너테이션
- 정적중첩클래스
- 인프콘
- github actions
- 비정적중첩클래스
- 자바의정석
- IoC
- 스파르타코딩클럽
- 스프링컨테이너
- privateapi
- 서버사이드렌더링
- Today
- Total
멈재
[Java] 정확한 답이 필요하다면 float와 double은 피하라 본문
Java에는 실수형을 나타내는데 기본적으로 float과 double을 지원한다.
float
- 4 바이트
- 정밀도 7자리
- 저장 가능 범위: 1.4x10^(-45) ~ 3.4x10^38
Double
- 8 바이트
- 정밀도 15자리
- 저장 가능 범위: 4.9x10^(-324) ~ 1.8x10^308
실수를 표현하는 방식으로는 고정 소수점 방식과 부동 소수점 방식으로 나눌 수 있다.
이러한 float과 double은 기본적으로 부동 소수점 방식을 사용한다.
고정 소수점과 부동 소수점
컴퓨터는 0과 1로만 이루어진 2진수 체계로 이루어져있다.
그렇기 때문에 실수 또한 2진수로 표현해야 한다.
참고: 컴퓨터는 왜 2진수를 기반으로 할까?
https://madplay.github.io/post/why-computer-is-based-on-binary-system
실수의 표현은 소수점의 위치를 표현하고 무엇이 정수 부분이고 실수 부분인지를 구분해야 하기 때문에 정수에 비해 상대적으로 복잡하다.
고정 소수점(Fixed-Point)
고정 소수점 방식은 소수점의 위치를 미리 지정해놓고(고정) 소수를 표현하는 방식이다.

위 이미지처럼 실수를 표현하는 32비트의 고정 소수점 방식이 있다고 가정해보자.
그리고 이 자료형은 1비트는 부호 비트로, 15비트는 정수부로, 나머지 16비트는 소수부를 사용한다.
이처럼 고정 소수점 방식은 소수점의 위치가 고정되어 있기 때문에 정수를 표현하는 것처럼 실수도 정수처럼 표현할 수 있다. 따라서 오차없는 정확한 계산이 가능하다는 장점이 있으나 표현 범위가 제한적이라는 단점을 가지고 있어서 잘 사용되지는 않는다.
부동 소수점(Floating Point)
반면에 부동 소수점 방식은 부호부, 가수부 그리고 지수부로 나뉘게 된다.
대부분의 부동 소수점 방식은 IEEE 754 표준을 따르고 있고 Java의 float과 double 또한 해당 스펙을 따른다.

기본 표현식은 -1^S x M x 2^E 으로 표현할 수 있으며 각각이 의미하는 바는 다음과 같다.
- S: 부호부(Sign) 1비트를 의미하며 0이면 양수, 1이면 음수가 된다.
- M: 가수부(Mantissa) 23비트를 의미하며 양의 정수로 표현한다.
- E: 지수부(Exponent) 8비트를 의미하며 소수점의 위치를 나타낸다.
부동소수점 변환 예시
숫자 -314.625를 IEEE 754 부동소수점 방식으로 표현하는 예시이다.
1. 부호부
부호가 음수이므로 32비트의 가장 앞자리는 1이 된다.
| 부호부 | 지수부 | 가수부 |
| 1 | - | - |
2. 가수부
숫자의 절댓값을 2진수로 표현한다. 314.625를 2진수로 변환하면 다음과 같다.
314 = 100111010(2)
0.625 = 0.101(2)
314.625 = 100111010.101(2)
이 이진수의 소수점을 소수점 왼쪽에 1만 남도록 이동시킨다.
100111010.101(2) --- from
1.00111010101(2) --- to
1.00111010101(2) x 2^8 --- result
그런 다음 소수점을 기준으로 오른쪽 부분(00111010101)을 가수부(23비트)의 앞에서부터 채우고 남는 공간은 0으로 채운다.
| 부호부(1비트) | 지수부(8비트) | 가수부(23비트) |
| 1 | - | 00111010101000000000000 |
3. 지수부
8에 bias를 더해준 다음 2진수로 변환한다.
지수는 8이므로 Bias를 더해야 한다.
32비트 IEEE 754 형식에서 Bias는 2^(k-1)로 구할 수 있으며 k는 지수부의 비트수를 나타낸다.
따라서 Bias는 127(2^(8-1))이므로 8 + 127 = 135이 된다.
135를 이진수로 변환(10000111(2))한 다음 8비트 지수부에 채워준다.
| 부호부(1비트) | 지수부(8비트) | 가수부(23비트) |
| 1 | 10000111 | 00111010101000000000000 |
위와 같은 과정을 통해 -314.625를 부동소수점 방식으로 표현하면 11000011100111010101000000000000으로 나타낼 수 있다.
이 링크에서 간편하게 숫자를 부동소수점으로 변환해 볼 수 있습니다.
이와 같은 방법은 소수점이 고정되지 않으므로 폭넓은 범위를 표현할 수 있지만 오차가 발생하기 때문에 근사치로 표현한다고 이해해야 한다.
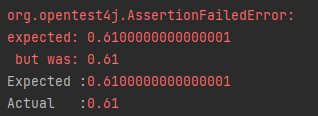
부동 소수점 방식인 double로 연산을 수행하게 되면 정확한 결과값을 얻을 수 없다.
1.03 달러에서 42센트를 사용했을 때의 계산을 수행하게 되면 테스트가 실패하게 된다.
@Test
void 부동_소수점_연산_결과() throws Exception {
double dollar = 1.03;
double cent = 0.42;
double rst = dollar - cent;
assertThat(0.61).isEqualTo(rst);
}
올바른 방안
이러한 문제를 올바르게 해결하려면 BigDecimal이나 int, long을 사용해야 한다.
1) BigDecimal
public class BigDecimal extends Number implements Comparable<BigDecimal> {
...
private final BigInteger intVal;
private final int scale;
private transient int precision;
...
}- BigInteger intVal: 정수, 정수를 저장하는데 사용한다.
- int scale: 지수, 소수점 첫째 자리부터 끝나는 위치까지의 총 소수점 자리수
- int precision: 정밀도, 수가 시작하는 위치부터 끝나는 위치까지의 총 자리수
@Test
void 부동_소수점_연산_결과() throws Exception {
BigDecimal bigDecimal = BigDecimal.valueOf(1234.56789);
System.out.println(bigDecimal.unscaledValue()); // 123456789
System.out.println(bigDecimal.scale()); // 5
System.out.println(bigDecimal.precision()); // 9
assertThat(bigDecimal).isEqualTo(new BigDecimal("1234.56789"));
}
BigDecimal 클래스는 생성자와 파라미터로 문자열을 넘겨 생성하는 것이 일반적이지만 정적 팩터리 메서드도 제공한다.
@Test
void 부동_소수점_연산_결과() throws Exception {
BigDecimal value1 = new BigDecimal("1.03"); // 생성자
BigDecimal value2 = BigDecimal.valueOf(0.42); // 정적 팩터리 메서드
BigDecimal rst = value1.subtract(value2);
assertThat(rst).isEqualTo(new BigDecimal("0.61")); // Test passed
}
주의해야 할 점은 BigDecimal을 생성할 때 생성자를 사용할 경우 문자열이 아닌 double 타입을 넘기면 안된다는 것이다.

BigDecimal은 기본 타입보다 쓰기 불편하고 느리다는 단점이 있다.
2) 정수형 int와 long을 이용
성능이 중요하고 소수점을 직접 추적할 수 있고 숫자가 크지 않다면 int나 long을 쓸 수도 있다. 이 경우에는 다룰 수 있는 값의 크기가 제한되고, 소수점을 직접 관리해야 한다.
숫자가 9자리 10진수로 표현할 수 있다면 int를 사용하고, 18자리 10진수로 표현할 수 있다면 long을 사용하고, 그 이상인 자릿수라면 BigDecimal 사용을 권장한다.
참고
'JAVA & Spring & JPA' 카테고리의 다른 글
| [디자인 패턴] 싱글턴 패턴, 내가 알던 싱글턴이 아니야! (0) | 2023.04.18 |
|---|---|
| [JAVA] 자바 애너테이션과 활용 예시 (Annotation) (0) | 2023.03.26 |
| [JAVA] 20. 동일성(identity)과 동등성(equality) (0) | 2023.01.08 |
| [JAVA] 18. 상속(IS-A) VS 구성(HAS-A) (0) | 2023.01.02 |
| [Spring/JPA] 14. AttributeConverter로 코드의 가독성을 높여보자 (0) | 2022.12.20 |




